sequence to calculate gravity - Gravity explored
Hoofdmenu:
sequence to calculate gravity
sequence to calculate gravity
Introduction
Calculating Gravity can be done in 5 steps.
Step 1) Coulombforce
Consider the interaction between a proton and electron within a hydrogen atom and calculate the amount of Coulomb force between the proton and neutron.
The Coulombforce in an atom equals the centripetal force ( force directed inwards to the center)
Step 2) Mass electron
Based on the calculated Coulombforce which acts as centripetal force and the centrifugal force as opposite force the mass of the elektron can be calculated.
Step 3) Integration of Kepler's Law, Coulomb's law, Centrifugal force and gravity
There is an analogue here. Kepler's Laws are describing the path of planetary motion. The centripetal force in Kepler's laws is the gravitation force as defined by Newtons law of attraction.
Inside the hydrogen atom the centripetal force is the Coulomb force as defined by Coulombs law. For both situations (Kepler and Coulomb) the centripetal forces are in equilibrium with their centrifugal forces.
This is interesting because in both cases centrifugal forces (planetary and ”proton/electron” scale) are physical identical and both contain acceleration generated by the centripetal force. Acceleration can be described as a vector. Like gravity the acceleration vectors have the dimension (m/s^2). This creates a situation where acceleration vectors and the gravity field strength are fully complementary.
So this clears the path for gravity to interfere with the centrifugal force of the electron and therefore influencing its equilibrium with the Coulomb force inside the atom.
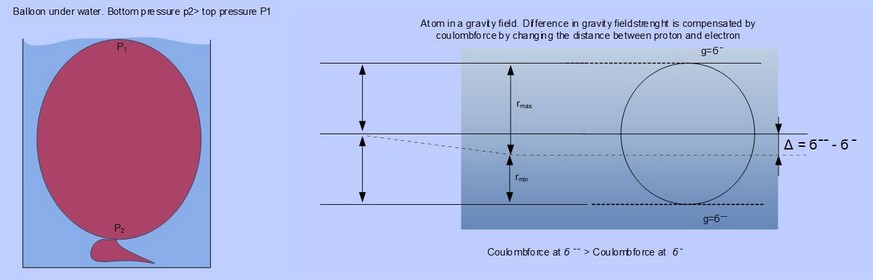
Compare the atom in a gravitational field with a balloon under water. The atom represents the balloon and the water represents a gravity field. The deeper the balloon gets submerged the higher (more gravity) the pressure on the balloon. The balloons inside pressure will increase to match the increasing outside pressure, so also with the atom. In similarity the gravity field strength is influencing the distance between the proton and the electron and thus influencing the diameter of the atom
This implies a lot. It would mean that this affects our experienced space-time frame. An example: Say we have a chain of atoms with a length of 1 meter on earth’s surface. We put this chain of atoms in orbit around the Earth at a height of 20.200 km ( height where the GPS satellite are orbiting the earth). The gravity is reduced to appr. 0.56m/s^2. Our "meter of atoms" has an increased relatively length because of the change in distance between all the electrons and protons in this "meter of atoms" causing a relative change in diameter of the atoms. Every day the satellite travels around 78cm more than noticed. because it is rotating around the Earth and after exact 24 hours the distance doesn't match our reference ( earth's meter ) anymore. (See calculating time difference in the blog for full explanation and calculation)
How to examine the influence of gravity
Think of the balloon. When submerged just beneath the surface, the pressure on the top of the balloon is atmospheric, but on the bottom side of the balloon, the pressure is higher. This also occurs in a gravitational field, only the differences in gravitational fields are much smaller. So there is a need to define an infinite small parameter for gravity. “gravity operator” . A infinite small parameter can give a value for an infinite small change in the gravity field on atom sized scale.
With help of Newtons law and Earth’s mass it is possible to construct the gravity operator. See the tab of Gravity operator for full explanation
Newtons Law
With the atoms mass as m1 and r as the radius between earths center and the atom on earths surface.
Just like the force of gravity on Earth’s surface is depending on Earths radius , also is Earths mass related to its radius.
For Earths mass we can assume
Whith the knowledge of the infinite small change in gravity on earth's surface, it is possible to find the small change in gravity acting on the atom. The small difference is interfering with the forces within the atom. The atom adapts by changing the distance between the proton and the electron on a way that equilibrium between Coulomb force and centrifugal force is maintained. This can be arranged by changing the radius between proton and electron. Smaller distance between the particles increases Coulombforce
With help of the coulomb force acting between the proton and the electron in an atom in a gravitational field it is possible to find a value for the radius at the top and at the bottom of the atom.
The value of these radii can be found with use of Keplers law. See the tab of Kepler’s law for full explanation
The change in radius of the atom is very small. To make calculations possible, 20 digits are used.
Values for "minimum radius", where gravity field is highest and "maximum radius", where gravity field strength Is lowest are
Step 4)
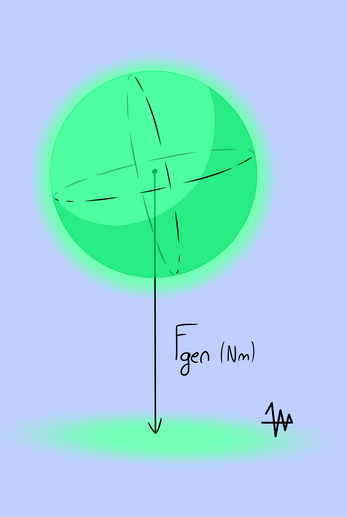
When absorbing the gravitational field into the atom, as reaction the distance between the electron and the proton changes. The influence of change in distance between the proton and the electron is different for the Coulomb force as Centripetal force in relation to the centrifugal force. See Tie-graph for more explanation. With a small deviation in radius the electrons trajectory will be eccentric shaped. This means centrifugal forces are not constant and the result is a generated force (Fgen).
In a constant gravity field this generated force also will be directed.
The net value for the generated force ( Fgen) of the electron is pulling on the proton and the result is a total directed force in Nm for the atom. The amount of change in Coulomb force/ centripetal force is “like the balloon submerged under water” opposite to maintain equilibrium. But the atom has free rotation and acts like an polar magnet to complete the equilibrium in the gravity field.
Now with the generated force "directed" the atom shows acceleration produced by Fgen. When we stop the atom we experience this force as weight or mass.
The Newton meter is commonly known as torque.
Summary: At this point we calculated a force (Fgen) generated by the atom by adsorbing the gravitational field-strength. From this point on we can compare the generated force with the force (F) as used in Newton's second law.
A difference in approach here is that Newtons second law is based on the idea that mass is pulling on another mass. “The appel falls to the ground, pulled by gravity“, The force F has the dimension Newton
Fgen however contains a force in Nm (Newton meter). This means this force is a torque. The electron has a constant pull on the proton and causes this torque.
When returning to our “famous apple” the acceleration in this theory is generated within the atom by continuous adsorbing the gravitational field strength. In other words, the apple travels by itself.
With this in mind and with the use of Newtons second law, we can define 
The generated force is created as a product from angular impulse with acceleration.
(The net torque acting over a time interval is the angular impulse.)
For a rotating point mass ( like the electron) the inertia (I) is
With the continuous gravitation field, the generated rotational inertia will also be continuous.
The speed of the electron is also depending on the radius . The speed can be found with
Our calculated mass of the atom has compared to the real defined mass 1.672623*10-27an offset of 0.868 %
When checking the dimensions, mass of the atom has the dimension 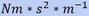
The difference in dimensions of mass is caused by how to look to this system. When mass is pulling on another mass then mass has the dimension  and it can’t create acceleration by itself.
and it can’t create acceleration by itself.
Who knows? Is this the missing link and another step forward?